CEC’2022 Competition on Heat Pipe-Constrained Component Layout Optimization
Important Announcement:
Thank you all for your participation in our CEC2022 HCLO competition! After a comprehensive evaluation in our private test problem 5, we would like to announce the final result here. Congratulations to winners!
- Winner: NBEA_VNS, Zhiyun Deng, Shichen Tian, Jiaxin Fan, Liang Gao, Weiming Shen, Huazhong University of Science and Technology (Prize: $500)
- First runner-up: CBBPGA, Helan Liang, Haoran Ye, Tao Yu, School of Computer Science and Technology, Soochow University
- Second runner-up: Enhanced-RACOS, Haohan Huang, Dong Zhang, Huawei, GTS, ATD
Results will be officially announced in the competition session of WCCI2022 on 20 July (21:00 Beijing) (https://wcci2022.org/programs/#oral). The certificates of winners will be issued by IEEE soon.
| Rank | Algorithm Name | Authors | Affiliations | bestObj | meanObj | cons1 | cons2 | cons3 | cons4 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | NBEA_VNS | Zhiyun Deng, Shichen Tian, Jiaxin Fan, Liang Gao, Weiming Shen | Huazhong University of Science and Technology | 151.1667 | 152.5417 | 0 | 0 | 0 | 0 |
| 2 | CBBPGA | Helan Liang, Haoran Ye, Tao Yu | School of Computer Science and Technology, Soochow University | 153.0833 | 155.1071 | 0 | 0 | 0 | 0 |
| 3 | Enhanced-RACOS | Haohan Huang, Dong Zhang | Huawei, GTS, ATD | 155 | 156.2 | 0 | 0 | 0 | 0 |
| 4 | DDCMOEAPDen | Jing-yu Ji, Man-Leung Wong | Department of Computing and Decision Sciences, Lingnan University, Hong Kong | 155.5833 | 158.5944 | 0 | 0 | 0 | 0 |
| 5 | APCSH | Jiaqian Li, Genghui Li, Laizhong Cui, Zhenkun Wang | College of Computer Science and Software Engineering, Shenzhen University | 155.75 | 160.4889 | 0 | 0 | 0 | 0 |
| 6 | Algorithm | Ning Wu, Han Huang | School of Software Engineering, South China University of Technology | 156 | 161.5385 | 0 | 0 | 0 | 0 |
| 7 | MCZGA | Chengzhi Ma, Han Huang | School of Software Engineering, South China University of Technology | 156.25 | 160.0139 | 0 | 0 | 0 | 0 |
| 8 | SHCEA | Junfeng Tang, Yongcun Liu, Nan Zheng, Handing Wang | School of Artificial Intelligence, Xidian University | 158.0833 | 164.8167 | 0 | 0 | 0 | 0 |
| 9 | cluster_moead | Zeyang Liu, Han Huang | School of Software Engineering, South China University of Technology | 158.1667 | 164.8056 | 0 | 0 | 0 | 0 |
| 10 | bupt_wanxing | Xing Wan | School of Computer Science, Beijing University of Posts and Telecommunications | 159.8333 | 163.7333 | 0 | 0 | 0 | 0 |
| 11 | GA | Shulei Liu, Chao Li, Xu Liu, Jialiang Sun, Handing Wang | School of Artificial Intelligence, Xidian University | 160.1667 | 171.3806 | 0 | 0 | 0 | 0 |
| 12 | DGPCOA | Qian Wang, Qinghua Gu, Lu Chen, Yufeng Zhou, Xuexian Li | School of Management, Xi’an University of Architecture and Technology | 160.75 | 174.6333 | 0 | 0 | 0 | 0 |
| 13 | Ant | Jie Li, Yuxin Xu, Chumei Gu, Yuan Zhuang, Jianjun Cao, Nianfeng Wen | Information quality research group, The 63rd Research Institute, National University of Defense Technology | 162.5833 | 166.6914 | 0 | 0 | 0 | 0 |
| 14 | BEE_LOTS | Jiale An, Yang Gao, Penghui Tan | Southwest University of Science and Technology | 162.9167 | 169.4611 | 0 | 0 | 0 | 0 |
| 15 | CCSDG | Yu Liang, Han Huang | School of Software Engineering, South China University of Technology | 167.4167 | 178.5317 | 0 | 0 | 0 | 0 |
| 16 | our_work | Wu Song, Binghai Wang, Bo Liu, Tianqi Xu | Hainan Tropical Ocean University | 175.5833 | 189.8851 | 0 | 0 | 0 | 0 |
| 17 | GOA | Jianpeng Ye, Ming Lin | College of Computer and Information Sciences, Fujian Agriculture and Forestry University | 216.9167 | 227.7424 | 0 | 0 | 0 | 0 |
| 18 | GA_EDA | Ke Shi, Xinyue Li, Yu Zhang, Wang Hu | University of Electronic Science and Technology of China, School of Computer Science and Engineering | 161.3333 | Nan | 5657.625 | 0 | 0 | 0 |
| 19 | MSSADE | Tongli He, Han Huang | School of Software Engineering, South China University of Technology | 163.6667 | Nan | 18073469 | 0 | 0 | 0 |
| 20 | FDB_COLSHADE | Keke Jin , Qian Chen , Aihua Yin | Jiangxi University Of Finance And Economics | 0 | Nan | 27862225 | 0 | 0 | 9868.235 |
The performance of electronic devices is significantly influenced by the placement of its components. For example, an increasing number of electronic components are required to be installed within a small size of device space (such as print-circuit boards), thus easily causing a severe heat concentration. An irreversible device damage would probably happen under over-high temperature if their positions are not carefully arranged. Therefore, it raises an important practical engineering-driven optimization problem, the component layout optimization (CLO) problem. The objective of this problem is to maximize the thermal performance by optimizing the layout scheme of components while satisfying some necessary design constraints (including non-overlapping constraints, system centroid constraint, etc.). To obtain the global optimal component layout design, population-based evolutionary algorithms show their unique advantages over than gradient-based algorithms. However, the complexity in such problems still poses great challenges to common evolutionary optimization algorithms.
Firstly, taking position coordinates as design variables, the CLO problem can easily become a high-dimensional optimization problem with the number of components increases. Secondly, a huge number of complex constraints should be strictly satisfied. One type of basic geometric constraint is the spatial non-overlapping constraint between components or between the container and components, which requires that no overlap exists between any two objects. Thirdly, there may exist two or more distinct component layout design schemes corresponding to the same or similar performance, which makes the CLO a multimodal optimization problem. All these points make the CLO problem intractable in efficiently and effectively searching optimal or suboptimal layout solutions using common evolutionary algorithms, which highly hampers their industrial applications. The aim of this competition is to promote the research on continuous constrained single-objective optimization problems and hence solve complicated real-world application problems.
In this competition, one typical layout design scenario, the Heat pipe-constrained Component Layout Optimization (HCLO) problem, is carefully selected and simplified from the real-world engineering layout application. As shown in Figure 1, the largest red rectangle denotes the layout container, determining the available layout domain boundary. Green rectangles mean heat pipes where the generated heat by components can be directly dissipated outside by heat conduction. Blue shaded boxes represent the electronic components that are required to be placed right above the heat pipes and within the layout domain. The design objective is determined to minimize the maximal real heat dissipation power of heat pipes, that is, to improve the heat dissipating uniformity among all heat pipes. Therefore, the HCLO problem is a continuous constrained single-objective optimization problem. Note that the source code for calculating the relevant performance indicators will be provided in two programming languages (MATLAB and Python). Researchers can choose to use either of them for convenience.
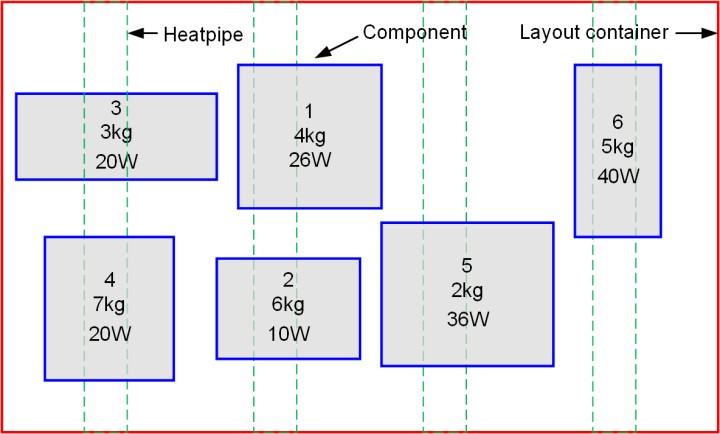 |
|---|
| Figure 1. The illustration of Heat pipe-constrained Component Layout Optimization (HCLO) problem |
In this competition, there are five HCLO problems with different optimization scales under different problem settings: four public HCLO problems and one private HCLO problem. Four of them are public, which will be totally uncovered to help participants to better understand this task, and develop effective and efficient layout search algorithms. The last one is private with the same problem type, where the evaluation code involved will not be released. Participants are encouraged to develop the algorithm to solve this type of optimization problem, not just specific one of them. Participants may propose a new optimization algorithm or utilize a hybrid form of previously proposed algorithms. However, it must be restricted in the field of evolutionary computing. Besides, using commercial optimization software is not allowed. Participants are required to submit their own source codes along with a brief description of the optimization algorithm, as well as a brief code instruction. The performance evaluation of your proposed algorithm will be carried out in the private HCLO problem by organizers to guarantee its fairness. With the same computational budget, the best layout solution of each problem obtained by randomly running your algorithm several times will be compared directly. To fairly assess the performance of compared algorithms, we will directly evaluate the objective value of the best layout design when all constraints are satisfied. If no feasible solution is returned when the termination condition is satisfied, their constraint violations will be compared. The algorithm with less constraint violation will be better.
A brief problem description:
As shown in Figure 1, the design variables of this problem are their two-dimensional position coordinates. In order to meet the requirement of heat dissipation and system mass characteristic, four types of design constraints are established. One is the basic geometric non-overlapping constraint, which requires that any two components cannot overlap and any component cannot protrude from the layout domain. The second constraint is that the system centroid should be controlled below a specific absolute error with the expected centroid. The third one is involved in the heat dissipation process, which requires that components must overlap with heat pipes. Only if components intersect with heat pipes, the generated heat can be transferred outside, avoiding heat concentration. Note that for each heat pipe, there is a maximal heat-dissipating power capacity. Therefore, the summation of heat-generating power of components that are placed above each heat pipe should not exceed its maximal capacity, which is the last constraint. When one component occupies two heat pipes simultaneously, it is assumed that its thermal power is equally conducted to two heat pipes. It is desired that the heat distribution over this layout area should be uniform. For simplification, the design objective is determined to minimize the maximal real heat dissipation power among all heat pipes. To summarize, the HCLO problem is a continuous constrained single-objective optimization problem. Four public HCLO problems are introduced briefly below.
- Problem 1 (Public): 6 components need to be placed properly within one layout domain, involving 12 design variables.
- Problem 2 (Public): 15 components need to be placed properly within one layout domain, involving 30 design variables.
- Problem 3 (Public): 40 components need to be placed properly within two layout domains, involving 80 design variables.
- Problem 4 (Public): 90 components need to be placed properly within four layout domains, involving 180 design variables.
Problem Statements and codes:
The detailed problem statement for this competition can be downloaded here. Codes for evaluating four public test problems are supplied with two versions (MATLAB and Python). Accordingly, submissions of MATLAB or Python source codes are both acceptable.
Rules:
- Participants will propose and implement metaheuristic algorithms (e.g., evolutionary algorithms, swarm intelligence, estimation of distribution algorithm, etc.) to solve complex problems in the layout design domain.
- The code for evaluating the objective and constraints is strictly not allowed to be changed.
- A maximum number of 5000D function evaluations is allowed (D means the dimension of design variables).
- Only random seed initial solutions are allowed in this competition. Heuristics and special tweaks for initial solutions are not accepted.
Code Submission:
Please send your submission file (a zip file containing source codes, team information, etc.) directly to chenxianqi12@nudt.edu.cn. The code preparation should follow the style and format of the code example (MATLAB and Python).
Important Dates:
Deadline of code submission: May 1, 2022
CEC 2022 Conference: July 18-23, 2022
Organizers:
Wen Yao, Defense Innovation Institute, Chinese Academy of Military Science, China (Email: wendy0782@126.com)
Weien Zhou, Defense Innovation Institute, Chinese Academy of Military Science, China (Email: weienzhou@outlook.com)
Xianqi Chen, College of Aerospace Science and Engineering, National University of Defense Technology, China (Email: chenxianqi12@nudt.edu.cn)
Handing Wang, School of Artificial Intelligence, Xidian University, China (Email: wanghanding.patch@gmail.com)
If you have further questions, please do not hesitate to contact us by Email (chenxianqi12@nudt.edu.cn or other organizers), or move to our ISSUE BOARD for our competition.